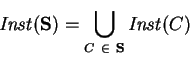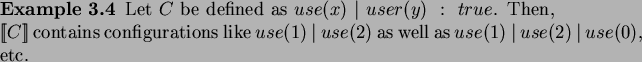

Next: A Symbolic Verification Procedure
Up: An Assertional Language for
Previous: An Assertional Language for
In order to finitely represent the generators of an upward
closed set of configurations, we use a rich assertional language
based on the notion of constrained configurations, i.e.
multisets of (non ground) atomic formulas annotated with
constraints.
Let
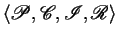 be an
be an
 specification,
with
specification,
with
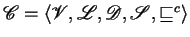 .
A constrained configuration is a multiset of atomic formulas
over
.
A constrained configuration is a multiset of atomic formulas
over 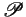 and
and 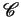 , annotated with a constraint, having the form
, annotated with a constraint, having the form
where
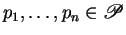 ,
,
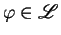 is a satisfiable
constraint, and
is a satisfiable
constraint, and
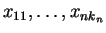 are distinct variables in
are distinct variables in
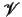 .
.
The set of ground instances of a constrained configuration can be
defined as follows.
Let
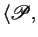
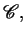
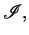
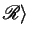 be an
be an
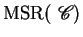 specification,
and
specification,
and
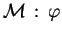 a constrained configuration. The set of ground instances
of
a constrained configuration. The set of ground instances
of
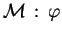 is defined as
is defined as
As an example, let 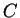 be the constrained configuration
be the constrained configuration
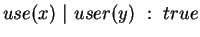 .
Then, if LC-constraints are interpreted over non-negative integers
.
Then, if LC-constraints are interpreted over non-negative integers
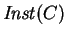 contains
configurations like
contains
configurations like
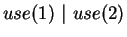 ,
,
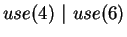 , etc.
, etc.
The previous definition can be extended to sets of constrained configurations
(denoted
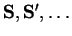 ) in the natural way:
) in the natural way:
Following the intuition we explained in the previous section,
instead of taking the set of instances as flat
denotation of a set of constrained configurations 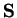 ,
we choose the following rich denotation.
,
we choose the following rich denotation.
Let
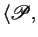
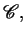
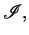
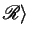 be an
be an
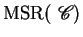 specification, and
specification, and 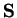 a set of
constrained configurations (with distinct variables from
each other). The rich denotation of
a set of
constrained configurations (with distinct variables from
each other). The rich denotation of 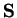 , denoted
, denoted
![$[\![{{\bf S}}]\!]$](img159.png) ,
is given by the upward closure of the set of its ground instances,
i.e.
,
is given by the upward closure of the set of its ground instances,
i.e.
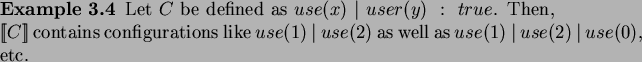


Next: A Symbolic Verification Procedure
Up: An Assertional Language for
Previous: An Assertional Language for
Giorgio Delzanno
2003-02-03