
Next: Symbolic Representation via Constrained
Up: An Overview of MSR():
Previous: An example: The Ticket
An Assertional Language for
Since we can easily encode the formalism of two counters machines
into
 , reachability problems are in general undecidable
for MSR(
, reachability problems are in general undecidable
for MSR(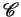 ) specifications.
Even for fragments of
) specifications.
Even for fragments of
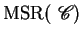 that are not Turing powerful, the
reachability set of an
that are not Turing powerful, the
reachability set of an
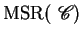 specification might be infinite and
thus it might be extremely difficult to explore it. The source of
infiniteness may be either the increasing size (number of
elements) of generated configurations, or the unboundedness
of the values attached to atomic formulas (e.g. think about
a simple counter incremented at every rule application), or both.
The only possibility of automatically analyzing the behavior of
this infinite-state specification consists of finding adequate
finite, symbolic representations of infinite collections of
configurations. In order to achieve this goal, in this section we
will introduce an assertional language based on the notion
of upward-closed sets of configurations.
To explain this idea, let us consider again the Example
1. Sup.pngpose we are interested in proving that the
specification of the example discussed in the previous sections
satisfies the following invariant: all reachable states satisfy
the mutual exclusion property only one process per time is in state use.
Instead of proving it directly, we can try to disprove it as
follows: we first select all possible configurations that violate
it, and then show that they are not reachable from the initial
state
specification might be infinite and
thus it might be extremely difficult to explore it. The source of
infiniteness may be either the increasing size (number of
elements) of generated configurations, or the unboundedness
of the values attached to atomic formulas (e.g. think about
a simple counter incremented at every rule application), or both.
The only possibility of automatically analyzing the behavior of
this infinite-state specification consists of finding adequate
finite, symbolic representations of infinite collections of
configurations. In order to achieve this goal, in this section we
will introduce an assertional language based on the notion
of upward-closed sets of configurations.
To explain this idea, let us consider again the Example
1. Sup.pngpose we are interested in proving that the
specification of the example discussed in the previous sections
satisfies the following invariant: all reachable states satisfy
the mutual exclusion property only one process per time is in state use.
Instead of proving it directly, we can try to disprove it as
follows: we first select all possible configurations that violate
it, and then show that they are not reachable from the initial
state 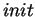 . The set of interesting violations
. The set of interesting violations 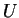 consists of
configurations like
consists of
configurations like
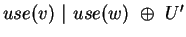 where
where 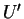 is any possible multiset. Then, we note that
is any possible multiset. Then, we note that 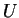 can be
generated from the (infinite) set of configurations
can be
generated from the (infinite) set of configurations
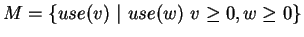 by taking the upward closure with
respect to multiset inclusion: if a configuration contains any
ground instance of
by taking the upward closure with
respect to multiset inclusion: if a configuration contains any
ground instance of 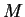 , then it violates itself the invariant.
As discussed in [1], the negation of an invariant
property often enjoys the property of being upward closed with
respect to an inclusion ordering defined over sets of
configurations.
As a first approximation of the problem of exploring an infinite
state space, we could then start the exploration from the unsafe
states, using minimal violations to represent them, and reason
backward by applying the predecessor operator
, then it violates itself the invariant.
As discussed in [1], the negation of an invariant
property often enjoys the property of being upward closed with
respect to an inclusion ordering defined over sets of
configurations.
As a first approximation of the problem of exploring an infinite
state space, we could then start the exploration from the unsafe
states, using minimal violations to represent them, and reason
backward by applying the predecessor operator 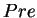 (i.e.,
computing weakest pre-conditions).
Let us formally define the notion of upward closed sets.
(i.e.,
computing weakest pre-conditions).
Let us formally define the notion of upward closed sets.
Let
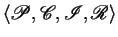 be an
be an
 specification, and
specification, and
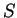 a set of configurations. The upward closure of
a set of configurations. The upward closure of 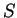 ,
denoted
,
denoted
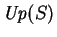 , is defined as
, is defined as
We say that 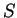 is
upward closed if
is
upward closed if
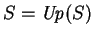 .
Upward-closed sets of configurations have interesting properties
with respect to the predecessor operator
.
Upward-closed sets of configurations have interesting properties
with respect to the predecessor operator 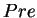 .
.
![\begin{proposition}[\cite{Del02}]
$Up(Pre(S))\subseteq Pre(Up(S))$\ for any set $S$\ of configurations.
\end{proposition}](img136.png)
In general the reverse implication does not hold.
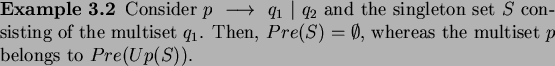
However, the following property holds.
![\begin{corollary}[\cite{Del02}]
If $S$\ is upward-closed, then $Up(Pre(S))=Pre(Up(S))$.
\end{corollary}](img138.png)
In other words, the class of upward-closed sets of configurations
is closed under the computation of the pre-image. The previous
properties do not suffice to finitely represent and manipulate sets
upward closed sets of configurations. In fact, we still have to
solve the problem of finitely represent what we called the
minimal violations.
This is not always possible. However, in the example of the
single server ticket algorithm
they have a regular structure that we can exploit by
translating the extensional description
into the following intensional
description, called a constrained configuration
where 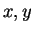 are free variables.
In other words, by annotating a non ground
configuration (i.e., in which formulas have free variables) with a
constraint we can implicitly represent all unsafe configurations we
are interested in for our example. They will correspond to the
upward closure of the set of ground instances of the constrained
configuration above. It is important to note that this techniques
is just an heuristics through which we try to embed as many
configurations as possible inside a regular structure. In the
following section we will formalize these ideas and show how to
use them in combination with the backward reachability approach
proposed in [1].
are free variables.
In other words, by annotating a non ground
configuration (i.e., in which formulas have free variables) with a
constraint we can implicitly represent all unsafe configurations we
are interested in for our example. They will correspond to the
upward closure of the set of ground instances of the constrained
configuration above. It is important to note that this techniques
is just an heuristics through which we try to embed as many
configurations as possible inside a regular structure. In the
following section we will formalize these ideas and show how to
use them in combination with the backward reachability approach
proposed in [1].
Subsections


Next: Symbolic Representation via Constrained
Up: An Overview of MSR():
Previous: An example: The Ticket
Giorgio Delzanno
2003-02-03