

Next: An example: The Ticket
Up: Constraint Multiset Rewriting
Previous: Constraint Systems
The
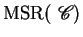 language
language
In the following we will use the notion of multisets. We use
 and
and  to denote multiset union and
multiset difference, respectively.
to denote multiset union and
multiset difference, respectively.
Let 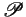 be a finite set of predicate symbols, and
be a finite set of predicate symbols, and 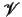 a denumerable set
of variables. An atomic formula over
a denumerable set
of variables. An atomic formula over 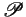 and
and 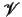 has the form
has the form
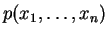 (with
(with 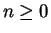 ), where
), where
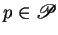 , and
, and
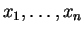 are distinct variables in
are distinct variables in 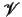 .
.
Now, let 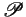 be a finite set of predicate symbols, and
be a finite set of predicate symbols, and 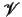 a denumerable set
of variables. A multiset of atomic formulas
a denumerable set
of variables. A multiset of atomic formulas 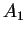 , ...,
, ..., 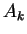 (with
(with 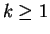 )
over
)
over 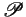 and
and 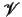 , is indicated as
, is indicated as
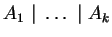 ,
where
,
where 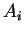 and
and 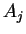 must have distinct variables for
must have distinct variables for 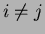 , and
, and
 is an associative and commutative constructor. The empty multiset is
denoted by
is an associative and commutative constructor. The empty multiset is
denoted by 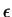 .
.
In the rest of the paper will use 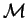 ,
, 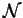 ,
,  to
denote multisets of atomic formulas.
to
denote multisets of atomic formulas.
Let 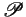 be a finite set of predicate symbols, and
be a finite set of predicate symbols, and
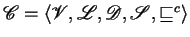 a
constraint system. An
a
constraint system. An
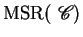 rule over
rule over 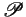 and
and 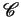 has the form
has the form
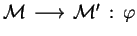 ,
where
,
where 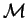 and
and
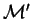 are two multisets of atomic formulas over
are two multisets of atomic formulas over 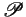 and
and 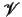 , with distinct variables, and
, with distinct variables, and
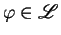 .
.
Note that
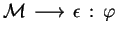 and
and
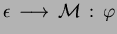 are possible
are possible
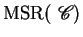 rules.
rules.
In order to make the intuitive semantics of the previous specification precise,
we introduce the ingredients for the operational reading of MSR rules.
We first define the notion of ground formulas.
Let  be a finite set of predicate symbols, and
be a finite set of predicate symbols, and
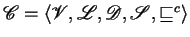 a
constraint system. A ground atomic formulas over
a
constraint system. A ground atomic formulas over 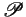 and
and 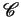 has the form
has the form
 (with
(with 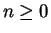 ), where
), where
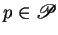 and
and
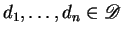 .
.
In the following, we will denote by
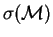 the
application of a solution
the
application of a solution
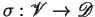 to a multiset
of atomic formulas
to a multiset
of atomic formulas 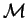 . Formally,
. Formally,
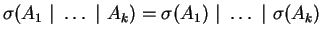 , and
, and
 if
if
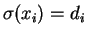 for
for
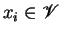 and
and
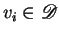 ,
, 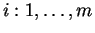 .
.
Given an
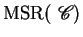 rule
rule
 , over
, over 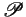 and
and 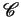 ,
the set of ground instances of
,
the set of ground instances of 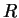 , denoted
, denoted
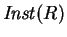 , is the set
of ground multiset rewrite rules defined as follows:
, is the set
of ground multiset rewrite rules defined as follows:
A central notion for our semantics is that of current configuration
given below.
Let 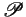 be a finite set of predicate symbols, and
be a finite set of predicate symbols, and
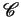 a
constraint system. An
a
constraint system. An
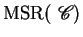 configuration
is a multiset of ground atomic formulas over
configuration
is a multiset of ground atomic formulas over 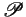 and
and 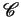 .
.
Configurations can be ordered with respect multiset inclusion as
follows.
Given two multisets of atomic formulas
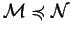 if
and only if
if
and only if
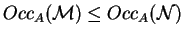 for every atomic
formula
for every atomic
formula 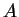 , where
, where
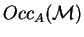 denotes the number of
occurrences of
denotes the number of
occurrences of 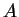 in
in 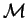 .
.
An
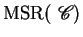 specification is defined as follows.
specification is defined as follows.
![\begin{definition}[$\mbox{MSR($\ {\mathscr C} $)}$\ Specifications]
An $\mbox{M...
...es over $ {\mathscr P} $\ and $ {\mathscr C} $.
\end{itemize}
\end{definition}](img82.png)
The operational semantics of an
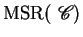 specification
specification
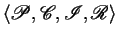 can be defined as follows.
Let
can be defined as follows.
Let 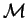 be a configuration.
A rule
be a configuration.
A rule
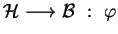 from
from 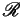 is enabled at
is enabled at  via the solution
via the solution
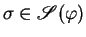 of the constraint
of the constraint
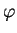 if and only if
if and only if
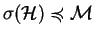 .
.
Now, sup.pngpose
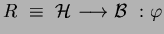 is enabled at
is enabled at 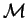 via
via
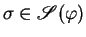 .
Firing this rule at
.
Firing this rule at 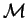 yields the new configuration
yields the new configuration
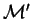 , written
, written
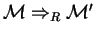 , if and only if
, if and only if
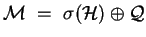 , and
, and
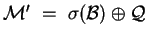 .
.
A run is a sequence of configurations
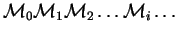 with
with
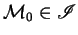 and for which
there exist
and for which
there exist
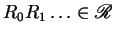 such that
such that
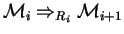 for
for 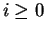 .
.
Let 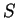 a set of configurations.
The successor operator
a set of configurations.
The successor operator 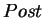 is defined as
is defined as
whereas, the predecessor operator 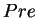 is defined as
is defined as
The reflexive and transitive closures of the predecessor and
successor operators are denoted 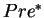 and
and 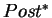 ,
respectively.
,
respectively.
The reachability set is defined as
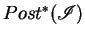 ,
, 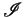 being the initial states of the
being the initial states of the
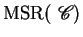 specification under consideration.
specification under consideration.


Next: An example: The Ticket
Up: Constraint Multiset Rewriting
Previous: Constraint Systems
Giorgio Delzanno
2003-02-03
![\begin{definition}[$\mbox{MSR($\ {\mathscr C} $)}$\ Specifications]
An $\mbox{M...
...es over $ {\mathscr P} $\ and $ {\mathscr C} $.
\end{itemize}
\end{definition}](img82.png)