I.U.M. Modellazione Geometrica

Corso di I.U.M. Modellazione Geometrica

NOTE AL LABORATORIO GUIDATO

Consideriamo tre problemi geometrici:

1. Orientamento di una terna di punti
2. Determinazione se un punto e' interno / esterno / sul contorno di un poligono convesso
3. (opzionale) Rasterizzazione di un poligono convesso

Algoritmo per problema 2 usa 1 come operazione ausiliaria. Algoritmo per problema 3 usa 2 come operazione ausiliaria.

Orientamento di una terna di punti

Una delle primitive geometriche forndamentali, usata come operazione primitiva in un problemi piu' complessi.

Dati tre punti A, B, C, da che parte giace C rispetto alla retta passante per A, B ed orientata da A verso B?

Risposte possibili:

C giace a destra di AB (la terna ABC definisce una svolta in senso orario),
C giace a sinistra di AB (la terna ABC definisce una svolta in senso antiorario),
C e' allineato con AB.

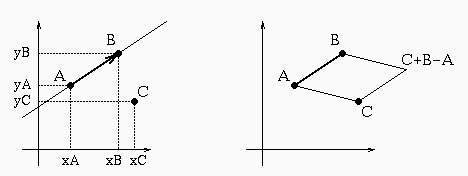
Vari modi di vedere il problema, portano tutti allo stesso algoritmo:

Modo 1. Prendere le coordinate di C, sostituirle nell'equazione della retta orientata AB, e vedere che segno ha il risultato.
Modo 2. Calcolare l'area con segno del parallelogramma di vertici B, A, C, (C+B-A) e vedere che segno ha.

Algoritmo 1 (con equazione della retta)

Equazione della retta orientata AB:
(x-xA)/(xB-xA) = (y-yA)/(yB-yA)
(x-xA)(yB-yA) - (y-yA)(xB-xA) = 0

Polinomio che si ottiene sostituendo le coordinate di C:
(xC-xA)(yB-yA) - (yC-yA)(xB-xA)

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Algoritmo 2 (con area del parallelogramma)

Si considerano i punti A=(xA,yA), B=(xB,yB), C=(xC,yC), D=C+B-A=(xD,yD)=(xC+xB-xA,yC+yB-yA), E=(xA,yD), F=(xD,yA).

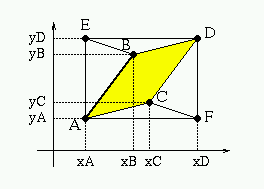
Area del parallelogramma ABDC = area del rettangolo AEDF - aree dei triangoli EAB, EBD, AFC, CFD (tutte aree con segno).

Area(AEDF) = (xD-xA)*(yD-yA) = (xC+xB-2xA)*(yC+yB-2yA).
Area(EAB) = Area(CFD) = 0.5*(xD-xC)*(yD-yA) = 0.5*(xB-xA)*(yC+yB-2yA).
Area(EBD) = Area(AFC) = 0.5*(xD-xA)*(yD-yC) = 0.5*(xC+xB-2xA)*(yB-yA).

Area(ABDC) = Area(AEDF) - 2*Area(EAB) - 2*Area(EBD) =
(xC+xB-2xA)*(yC+yB-2yA) - (xB-xA)*(yC+yB-2yA) - (xC+xB-2xA)*(yB-yA) = ...
... = (xC-xA)*(yB-yA) - (xB-xA)*(yC-yA).

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Conclusione

L'espressione di cui si valuta il segno e' il determinante

| yB-yA  yC-yA |
| xB-xA  xC-xA |

= (yB-yA)(xC-xA) - (yC-yA)(xB-xA)
= yA*xB - yB*xA + yC*xA - yA*xC + yB*xC - yC*xB

se e' minore di zero --> svolta a sinistra
se e' maggiore di zero --> svolta a destra
se e' uguale a zero --> allineati

Problemi numerici

Se il risultato e' molto piccolo in valore assoluto, puo' succedere che gli sia attribuito un segno errato a causa di errori di approssimazione inevitabili usando l'aritmetica floating point.

Una soluzione che di solito funziona e' quella di assumere una tolleranza epsilon>0 (molto piccola) e considerare come uguali a zero tutte le quantita' che in valore assoluto sono minori di epsilon.

In pratica si risponde che C e' allineato con A e B se la sua distanza dalla retta e' molto piccola, ovvero se l'area del parallelogramma e' molto piccola.

Complessita' temporale

Costante in quanto e' coinvolto un numero fissato di punti e di coordinate (3 e 6 rispettivamente).

Determinazione della posizione di un punto rispetto ad un poligono convesso

Siano P1, P2, P3, ..., P(n) i vertici di un poligono convesso, ordinati in senso antiorario.
Sia Q un altro punto. Qsta dentro, fuori, o sul contorno del poligono?

Q giace dentro il poligono se Q giace a sinistra di tutte le rette orientate passanti per lati del poligono (la retta orientata da P(i) a P(i+1), per ogni i da 1 a n).
Q giace fuori dal poligono se Q giace a destra di almeno una delle rette orientate sopra dette.
Q giace sul contorno del poligono se Q e' allineato con almeno una delle rette sopra dette, e giace a sinistra delle rimanenti. In particolare:
- se Q e' allineato con una e a sinistra delle altre, allora Q giace all'interno di un lato
- se Q e' allineato con due e a sinistra delle altre, Q coincide con un vertice
- non sono possibili altri casi.

Complessita' temporale

O(n) dove n e' il numero di vertici (o, equivalentemente, di lati) del poligono.

Nel caso peggione (punto interno o sul contorno), si riduce ad esattamente n chiamate alla primitiva che controlla l'orientamento di una terna di punti. Ciascuna chiamata ha un costo costante.

Rasterizzazione di un poligono convesso

Viene qui proposta una soluzione (solo "una" soluzione, non "una soluzione efficiente") all'esercizio 1 del capitolo 1 delle dispense, nel caso particolare di un poligono convesso.

Sono dati:

un poligono convesso i cui vertici, ordinati in senso antiorario, sono P1, P2, P3, ..., P(n).
una griglia di riferimento a celle (pixel) quadrate, definita dalle famiglie di rette orizzontali y=I e verticali x=J al variare di I, J nell'insieme dei numeri interi.

Si chiede di determinare quali celle della griglia sono intersecate dalla regione poligonale avente come contorno il poligono dato.

Assunzioni

Si assume che le coordinate dei vertici del poligono abbiano parte decimale non nulla. In questo modo evitiamo i casi particolari di vertici del poligono che cadono sul lato comune di due celle, o sul vertice comune di quattro celle della griglia.

Algoritmo

Ci sono tre tipi di pixel intersecati:

pixel che contengono un vertice (rossi in figura)
pixel che sono attraversati da un lato (verdi in figura)
pixel che sono contenuti interamente all'interno della regione (gialli in figura)

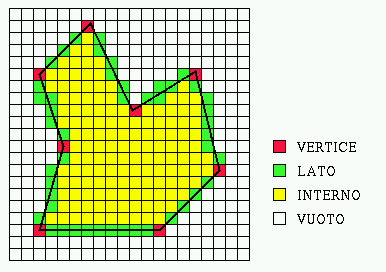
Pixel del primo tipo

Per ogni vertice P(i) del poligono, il pixel contenente P(i) si determina semplicemente calcolando la parte intera inferiore e superiore delle coordinate x ed y di P(i).

Pixel del secondo tipo

Questi pixel hanno almeno un vertice giacente all'interno del poligono ed almeno un vertice giacente all'esterno del poligono.

Pixel del terzo tipo

Questi pixel hanno tutti e quattro i loro vertici giacenti all'interno del poligono.

Metodo di calcolo unificato per i pixel di tipo 2 e 3

Per ogni vertice V della griglia (punto comune a quattro pixel), si determina se V giace dentro o fuori il poligono.
Non e' necessario esaminare tutti i vertici della griglia, ma solo quelli aventi coordinate x comprese fra la parte intera superiore del vertice piu' a sinistra e la parte intera inferiore del vertice piu' a destra del poligono, ed analogamente per le coordinate y. I rimanenti vertici della griglia cadono certamente fuori dal poligono.
Per ogni cella della griglia, si controlla lo stato dei suoi quattro vertici.
Se almeno uno di questi cade dentro al poligono, la cella interseca la regione poligonale.

Complessita' temporale

La determinazione delle celle di tipo 1 costa O(n) dove n e' il numero di vertici del poligono.
Per ognuno degli n vertici del poligono, occorre controllare la sua posizione rispetto ad un quadrato (poligono convesso di 4 lati), il che ha un costo in O(4) = O(1) cioe' costante.

La determinazione delle celle di tipo 2 e 3 richiede di esaminare due volte tutta la porzione di griglia le cui coordinate x ed y sono comprese fra le coordinate x ed y estreme del poligono dato (come spiegato sopra).
Supponiamo che questa parte di griglia sia formata da M1 pixel in orizzontale e da M2 pixel in verticale, vale a dire M1-1 vertici in orizzontale e M2-1 vertici in verticale.

Per ogni vertice di tale porzione della griglia, si controlla se e' contenuto nel poligono, operazione che costa O(n) nel caso peggiore.
Quindi, questo primo ciclo ha un costo in O(n (M1-1) (M2-1)) = O(n M1 M2).

Successivamente, per ogni cella in tale porzione della griglia, si controlla lo stato dei suoi quattro vertici, operazione che ha costo costante.
Quindi, questo secondo ciclo ha un costo in O(M1 M2).

La complessita' totale e' quindi in O(n M1 M2), ovvero in O(n M^2), dove M denota il massimo tra M1, M2.

Vedere qui per materiale di supporto (un esempio di input, un esempio di output, e un programma grafico che vi consentira' di visualizzare input e output per controllare la correttezza del risultato.